Review of Collisions

We reviewed yesterday's lesson again. It was on collisions. So, either elastic collision or inelastic collision.

Elastic collision- there is no change in kinetic energy after the collision has occured.

Inelastic collision- where some energy is 'lost' when colliding objects are in contact.

Mr. Banow showed us a whicked example of inelastic collision using two steel balls and a piece of paper.

First, he put one of the balls in the middle of a roll of tape and put the piece of paper on top of the ball. Next, he took the second ball and dropped it so it would hit the ball below the piece of paper.

What happened you may ask?

Well, a little hole was burnt into the piece of paper as well as a 'clunk' sound when the balls hit was made.

The reason why the collision of the two steel balls was inelastic because their was energy lost in the form of heat and/or sound. Not all of the energy was being conserved as kinetic energy.

We then did questions 1-4 on page 290.

Ryan Fly is up next.

Kinetic Energy

For some reason by pictures are up there ^^^^ but their relevance will be explained later. We started off class by reviewing the questions we started yesterday on power. These questions also reviewed calculating work quite nicely as we discovered that work needs to be calculated in order to solve for power.

Next, we expanded on what we had previously learned about energy. We we introduced to some new concepts:

1. Kinetic energy- the energy of motion. Ex: a ball rolling. Formula: $Ek=1/2mv^2$ Kinetic energy is a scalar quantity :)
2. Potential energy- the energy of rest. Ex: a ball being held in the air.
3. Change in energy= (final kinetic energy- initial kinetic energy) or $1/2(mvf^2-mvi^2)$

We learned that work= change in energy. This concept is important because it can make problem solving a lot easier. For example, we were given a problem that gave us the variables mass, initial velocity, and final velocity and were asked to solve for work. Instead of calculating force, displacement, and acceleration to eventually find work, we were able to simply calculate change in energy using $1/2(mvf^2-mvi^2).

Finally, we reviewed and expanded on our knowledge of collisions. We learned how energy fit into each type and were introduced to one new type:

• elastic collision- the two bodies don't stick together after the collision. There is no change in kinetic energy. Ex: the bat hitting the ball
• inelastic collision- the two bodies stick together after collision, some energy is lost. The energy lost is usually in the form of sound, heat, or light. Ex: the cars stuck together
• completely inelastic collision- the two bodies stick together after the collision but no energy is lost. Ex: the spaceship stuck in the planet.

Paige is next, I think.

Energy and Power

Monday we reviewed a bit of what we did on wednesday, we covered calculating work from a graph and when work is done by pulling something on a angle. We went over how work is produced: the force must be in the same direction as displacement to have work done.

What we learned on Monday was that when work is done, energy is transferred from one object to another. If the energy of an object increases, the work done on it will be positive. If the energy of an objects decreases, (ex. slowly bringing an object to the floor.) the work done on it will be negative.

Time has no effect when calculating work, but it does matter when we calculate power.

Power is the rate at which work is done and the rate at which energy is used. We calculate power in watts (W).... 1 watt is 1 J/s. Since watts are really small, we use kilowatts too (kW). To describe engines, the term horsepower is used. 1 horsepower equals 746 watts.

Things to Remember:

• P=W/t
• work is the product of force and the objects displacement (same direction)
• the less amount of time doing work, the more power being used (same displacement)
• to calculate kilowatt hours, multiply number of kilowatts by the number of hours used
• work is measured in joules (J)

Ex. 2. (in notes)

How much power is developed in lifting 82 kg of concrete to a height of 21 meters in 12 seconds?

m= 82kg
h= 21m (distance)
t= 12s
P=?
W=?
F=?

F= mg
F= 82kg x 9.80 m/s²
F= 803.6 N

W= Fd
W= 803.6N x 21m
W= 16 875.6J

P= W/t
P= 16 875.6J/12s
P= 1400W

Conservation of Momentum

The class began with the perpetual note-taking on the subject of Momentum; included in the aforementioned topic was the extended subtopic of the Conservation of Momentum. Various types of collision and explosion are included in the conservation of momentum—they are:

Explosion from Rest- One object splitting into multiple; given by the formula M1V1=-M2V2( and various manipulations of it).

Explosion from Motion-An object in motion, therefore with a initial velocity NOT of zero, splits into multiple objects; given by the formula (M1+M2)Vi=M1Vf1+M2Vf2

Elastic Collision-Two separate objects (with two separate masses and velocities) collide and rebound; given by the formula M1V1i+M2V2i=M1V1f+M2V2f

Inelastic Collision- Two objects colliding and becoming one; given by the formula M1V1i+M2V2i=(M1+M2)Vf

NOTE: All of these formulas can be derived remembering the Law of Conservation of Momentum, that is, initial momentum of an isolated system is equal to its final momentum, or the total momentum of an isolated system does not change.

Ex.)

A 95kg Unger collides while running 5.0m/s into a static Boss with a mass of 76kg. If Unger rebounds with a velocity of 3.0m/s, what is the velocity of the object he collided with?

M1V1i+M2V2i=M1V1f+M2V2f

M1=95kg

M2=76kg

V1i=5.0m/s

V2i=0.0m/s

V1f=3.0m/s

V2f=?

((95kg)(5m/s)-(95kg)(3.0m/s))/76kg=V2f=2.5m/s

We then continued with textbook questions on page 149, #1-5.

Whoever is left is next.

Momentum/Impulse

We started off class by finishing our notes from monday on Impulse. After we finished our notes we took up questions in our text books Page 243 #1-3.

Ex. What average force will stop a 1.0x10 3 car in 1.5s, if the car is moving at 22m/s?

m=1.0x10 3kg
deltaT=1.5s
vi=22m/s
vf=0
F=?

FdeltaT=mvf-mvi

F=-mvi/deltaT

F=-(1.0x10 3kg)(22m/s)/1.5s

=15,000N

When there was 10 minutes left in class Boss decided to take up more notes on
Law of conversation of Momentum
the total momentum of a closed system does not change.

An isolated system is one in which no net external force acts on the system
Momentum is conserved regardless of whether the iteractions exists in more than one dimension.

Then the bell rang and we ended off class with imcomplete notes that we will proabably take up today.

Mr. Banow has the power to pick who is next because i dont know who is left

Momentum

Momentum can be described as "inertia in motion." It is a vector quantity and the unit of momentum is kg * m/s.

Since the cannonball has more momentum than the cannon itself the cannon gets pushed backwards as the ball goes forward.

Ex.
What is the momentum of a 1.0x10^3kg car moving at 15m/s[E]?
m=1.0x10^3kg
v=15m/s[E]
p=?
p=mv
p=(1.0x10^3kg)(15m/s[E])
p=15000kg*m/s[E]

Impulse is simply the change in momentum. When an object experiences a force that causes it to speed up or slow down there is impulse.

When a golf club is about to hit a ball, the ball initially has zero momentum. After contact, the ball has momentum in the same direction as the force, and it also depends on how long the force acted upon the ball.

Ex.

What velocity will a 40.0kg child sitting on a 40.0kg wagon aquire if pushed from rest by a force of 75N for 2.0s?

m=40.0kg+40.0kg=80.0kg

F=75N

(delta)t=2.0s

Vi=0

Vf=?

F(delta)t=mvf-mvi

Vf=F(delta)t/m

Vf=(75N)(2.0s)/80.0kg

Vf=1.9m/s

Forces of Friction

We began by reviewing the subject matter from Friday, which concerned frictional forces...

• Static friction is defined as the friction that prevents a stationary object from beginning to move.
• Limiting static friction/Starting friction is defined as the maximum value of the force of friction that occurs just before the object starts to move.
• Therefore, if a force that is smaller than the limiting static friction is applied to a stationary object, the object won't move unless the force is increased and overcomes the limiting static friction, and once the object is in motion less force is needed to keep it in motion.
• is the formula used to determine the force of friction. As the mass increases, the Net Force increases, as well as the amount of friction.
• Without an applied force, a static frictional force does not exist.

We then did four examples that required us to utilize and manipulate the formulas concerning friction. Example one is shown below.

Ex.1) If the total weight of a skier and the skis is 500.0 N and a force of 35 N is needed to start the skier moving on the snow, determine the coefficient of static friction.

• We manipulate the formula to achieve 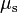= Ff/Fn
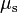• = 35 N/500.0 N
• Therefore, 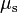= 0.070

Finally, we worked on practice questions from the textbook (Page 169, 1-4).

This link leads us to a video that explains the forces of friction in greater detail: http://www.youtube.com/watch?NR=1&v=cKUzHgBI_GY

Gbergz 360 is up next.

Friday November 4 - Frictional Forces

We started off class with a friday quiz on Newton's laws of motion, and then did some examples on the board.

After that we started talking about frictional forces. There are three kinds of frictional forces.

1) Static Friction - the friction that tends to prevent a stationary object from starting to move.

2)Limiting Friction - the maximum value of the force of friction which occurs just before the object starts to move. (starting friction)

3)Kinetic Friction: the force of friction that opposes the motion of a moving object. It is always less than the limiting static friction. (means that once the object starts moving the force of friction drops)

We then talked about the formula for the force of fricion $Ff=uFn$

u= Coefficient of friction (no unit)

Fn= Normal force (N)

Ff= Force of fricion

We finished the day talking about a problem with bricks and how the frictional force of a brick on its end is the same as a brick on its side.

Jolene is next.

November 4th Quiz Massacre!

The quiz results were not so great.  I am willing to Omit the quiz mark for you if you:

a. Fix up all of your quiz answers

b. Complete p. 156 #13, 17, 18.  These questions need to be answer clearly showing all of your steps and work.  I can't accept scribbles and the answer.

This must be submitted to me by Wednesday, November 9.  This will be a great way for you to re-practice this objective.

Gravitational Force

First we received our Newton's 2nd Law Investigation Labs, which we discussed why the %error was so high. We discovered that because we completely ignored the role of friction in the lab, it caused the over all result of the lab to be inaccurate. Mr. Banow than explained that we are to comment on his blog post and come up with a new and improved lab that will account for the friction.

We than began looking at Gravitational Force and learned three new definitions.

• Force of Gravity- objects are pulled toward the Earth no matter their location on or above the Earth's surface.



• Gravitational Field Constant- value is 9.8N/Kg and is represented by the letter g. This value is very close to being accurate anywhere on or near the Earth's surface.



• Gravitational Field Strength- the force of gravity is not the same everywhere therefore it is defined by the amount of force acting on a mass of 1Kg. For example there are different values on different planets.

Formula: F=mg

Example: The force of gravity on a 300.0Kg spacecraft on the moon is 489N. What is the gravitational field strength on the moon?

m=300.0Kg F=489N g=?

F=mg ----> g=F/m ----> g=489N/300.0Kg = 1.63N/Kg or 1.63m/s^2

Lastly we reviewed that mass and weight ARE DIFFERENT. Mass refers to the amount of matter in an object and stays the same no matter where it is. Weight describes the force of gravity on an object and changes depending on the gravitational field.

Jolene is next.

Newton's 2nd Law Lab - Going further!

In class we completed an investigation of Newton's Second Law.  Most of the data supported the fact that as the mass of the cart increased, the acceleration of the cart decreased.  Most of our data indicated that there was a lot of error in the calculated Net Force on the cart and the Theoretical Net Force acting from the mass hanging off the pulley.

Why was there so much error?

Could we do a new experiment to account for this error?

What would that experiment look like?  What could we add to the procedure?

Paige hasn't done this lab yet.  I need all of you in this class to be involved in a discussion about this topic.  Everyone must comment at least once on the questions above by this Friday.  Next week we will comment more and develop an experiment for her to do.  

• To start off the class we looked at Jeren's blog about Newton's third law of motion.


• We finished c) on example one of the notes finding out that we would add 22N to 121N to get 143N so it will overcome the force that is used by toboggan 2.


• We than got assigned practice questions on page 149, numbers 1, 2, 3a. Once done that we could finish assignment 6 that we got a few days ago. Once done those two assignments we could work on the review on page 155, numbers 8, 9, 11, 13, 17-20.

Page 149 Question #1

Two girls, one of mass 40 kg and the other of mass 60kg, are standing side by side in the middle of a frozen pond. One pushes the other with a force of 360N for 0.10s. The ice is essentially frictionless.

(a) What is each girl's acceleration?

Mg1-40kg Mg2-60kg Fa-360N T-0.10s

F=ma F/m=a 360N/40kg=a =9m/s^2 360N/60kg=-6m/s^2

(b) What velocity will each girl acquire in the 0.20s that the force is acting?

Vf=Vi+at =0+ 9m/s^2(0.10s)^2 = 0.9m/s

Vf=0+(-6m/s^2)(0.10s) = -0.60m/s

(c) How far will each girl move during the same time period?

d=Vi(t)+1/2(a)(t)^2 +1/2(9m/s^2)(0.10)^2 = 4.5 x10 ^-2 m

D=1/2(-6m/s^2)(0.10)^2 = -3.0 x 10 ^-2 m

2) Two crates of masss 12.0kg and 20.0kg, respectively, are pushed across a smooth floor together, the 20kg crate in front of the 12kg crate. Their acceleration is 1.75m/s^2. Calculate each of the following.

(a) the force applied to push the crates.

M1=12.0kg M2=20.0kg a=1.75m/s^2

F=(32.0kg)(1.75m/s^2) = 56.0N

(b) the action-reaction forces between the two crates.

F=(20.0kg)(1.75m/s^2) = 35.0N

Dana is next

Newton's Third and Best Law of Motion

• First of all, we got our quizzes back that we wrote unexpectedly on Friday then we learned about Newton's third law of motion which states: For every action force there exists a reaction force that is equal in magnitude but opposite in direction.
• After that we really didn't do much except a few examples on the third law of motion using F=ma and stating what the action or reaction was from an object doing something.

Ex: Badminton racquet hitting a birdie.

• Action: racquet force to birdie.
• Reaction: birdie applying force to the racquet.

Ex: Three toboggans are connected by a weightless, steel rope. The first toboggan has a mass of 75kg, the 2nd has a mass of 55kg, and the 3rd has a mass of 10.0kg. If the force exerted on the first toboggan is 310N and surfaces are considered to be frictionless, Find:

a) The acceleration of the toboggans.

F=ma changing the formula to a=f/m to find the acceleration. So it will be: a=310N/140Kg

=2.2m/s^2[E]

b) the force exerted by the toboggan two on toboggan three.

Again, F=ma in which F = ?, m = 10KG, and a = 2.2m/s^2 [E]

Therefore: F=(10KG)(2.2m/s^2[E])

=22N

c) the force exerted by toboggan one on toboggan two.

We will find out the true answer for this today in class, hopefully.

Blake is next.