Newtons Second Law of Motion

Today we started off by continuing the lab we started yesterday. We had put the force sensor on the dynamics cart and now it was time to collect some data! Mr Banow went over how to do the lab making sure to highlight some key points in the lab. Then we were off and racing. Lab Quests were procured and each group started collecting the data.

First off you were to use a motion as shown in the video and then we analyzed the force vs time graph and the acceleration vs time graph. Which we saw were quite similar. We then made a Force vs acceleration graph. When then curve fitted a line in the graph and got the equation of the straight line.

We saw that the Y corresponds with Force, the X with acceleration, M or the slope as mass and B the y-intercept should be zero.
Then using the linear-regression equation we determined acceleration given force.

After the trial runs were complete we completed the analysis questions in the lab and determined that

F=ma

Newtons Second Law of Motion!

Brittany is up next.

Inertia and Unbalanced Forces

In Tuesday's class be began by going over previous knowledge on how to draw Free-Body Diagrams. We then discussed various word problems, that allowed us to further understand how to draw and interpret free-body diagrams. After reviewing we progressed into the Law of Inertia.

Inertia, Newton's first Law of Motion, was originally derived from the ideas of Galileo. Inertia states that an object at rest will remain at rest and an object in motion tends to remain in motion, unless acted upon by an external force. More simply, objects keep doing what their doing unless acted upon by an unbalanced force. For example a stationary object is difficult to move, and a moving object is difficult to stop.

After various experiments including removing a tablecloth from under a place setting, we found inertia depends on mass.

Unbalanced Forces

Objects are typically acted upon by numerous forces simultaneously. 

• The resultant vector is called Net Force (Fnet)
• An objects velocity will remain constant if no external unbalanced force acts on it.
• If the forces acting on an object cancel out, the resultant vector is zero, and no unbalanced forces exist. Therefore the object is in equilibrium. 
• If an object is moving with a constant velocity, the net force is zero. 

The idea of unbalanced forces can be shown in the following example.

Ex. Two boys are pulling on a bear. One pulls with a force of 15N[E] while the other with a force of 10N[W]. What is the net force? 

<---10N[W]---Bear---15N[E]--->  Fnet= 5N[E]

Clarke is next! 

Fun with Forces

     In class we started a new unit called Newton's Laws of Motion and Forces. We started class by talking about what we new about Newton's laws and forces. 
      We found that force is a push or pull that may cause the object to:

• change its shape
• accelerate
• or not change in any way

We also found that there are four types of force which are:

1. Applied Force- is a force applied to an object by another object
2. Force of Gravity- Fg= 9.8 m/s2 which the downward force exerted on objects on earth
3. Normal Force- the force applied to an object which is on another stable object (ex. labquest on a table)
4. Friction Force- is a force applied to an object by a surface as it either moves or tries to move across that surface.

     We also started to learn how to draw free body diagrams, which allow you to show the forces applied to an object. 
Ex. Draw a free body diagram for a Hemi Cuda driving west on the highway. 

The Cuda has the forces of gravity, normal, friction and applied so the free body diagram would look like

We will be continuing to learn about free body diagrams in the next class.

Next is Indianna.

Continuation With Relative Motion

On Wednesday's class we continued learning about relative motion by doing examples. We then learnt how to do examples where a person or object wishes to move directly to the opposite side from their starting point. In order to do this we must figure out the direction the person or object should go by using trig functions. Here is one of the examples we did yesterday in class.

We then finished class with doing similar questions in the text book.

Shelby is next.

Relative Motion

In tuesday's class we learnt how to calculate problems that involve relative motion. Relative motion is when an object is moving compared to some frame of reference which is also in motion. We then watched videos on some examples such as ducks in the wind and an endless pool.

We then did some examples.

Plane is travelling 200km/h in the air. Wind is blowing 50km/h towards the west. Determine the velocity of the plane in terms of the ground if the plane moves west.

    pVa= pVa + aVg
          = 200.km/h [W] + 50. km/h[W]
          = 250 km/h[W]

If the distances being added are not collinear we would solve them like the vectors we have been doing for the past couple days. We would draw a diagram, solve for the missing side, then solve for the missing angle.





Casey is next.

Vector Resolutions!

On Friday's class we first practiced finding X and Y components of vectors. By breaking down the vectors into these components we are able to add them algebraically!!
For the X component we use the trig function cos, and for the Y component we use sin.

We practiced how to find the components for the rest of the class and started working through our step booklet to figure out problems needing vector resolution.
Vector resolution must be used when vectors are not perpendicular to each other. The steps to find vector resolutions in problems such as these are:

• find the angle of each vector by measuring counterclockwise from the x-axis (this step will prevent sign confusion later on)
• find each vectors X and Y components (formula examples are above)
• add collinear vectors algebraically  (add the X components of each vector together-the direction will be East if the answer is positive and West if the answer is negative; add the Y components of each vector together-the direction will be North if the answer is positive and South if the answer is negative)
• use the Pythagorean Theorem to find the magnitude of the resultant vector

• use a trigonometric ratio to find the angle of the resultant vector (tan is used for this step- tan=opposite/adjacent)
• by using the answers from the previous two steps and example would like like: 23m[E42degreesN]

After working through the booklet we practiced the new steps and did some textbook questions, which are due today !! 

Tyrell is up next!

Adding Non-Collinear Vectors Algebraically and Vector Resolution

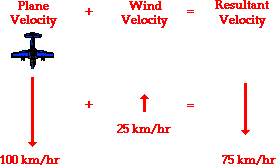
Today in class, we learned about adding non-collinear vectors without using Scale Diagrams (or without using the "tail-to-tip" method). 

You can add them together and find the Resultant Vector by using the Pythagorean Theorem and Trig Ratios. You can only use this if the two non-collinear vectors you are adding forms a right triangle. The formulas you can use for this are: 

Ex.) 92 m/s [W] + 115 m/s [S]

Solution: 

             Use the formula AR^2 = Ax^2 + Ay^2 to find AR.

             

                                    AR^2 = (92 m/s [W])^2 + (115 m/s [S])^2

                                              = 8464 + 13225

                                              = 21 689 (take the square root)

                                       AR  =  147m/s

           

             After finding AR, use the Trig Ratio formula to find pheta.

                 we find that pheta = 51.3 degrees

                The final answer is 147 m/s [W 51degrees S]

We also talked about multiplying a vector by a scalar. The units of both the vector and scalar quantities have to be multiplied and both units from each quantity becomes the unit in the product of the final answer.

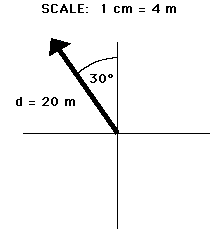
Before the class ended, we also started talkig about Vector Resolution. If you have two vectors that are not perpendicular (or does not form a right triangle), you can still add them algebraically by separating or breaking down the vectors into their own x and y components. After doing that, you need to use the trig ratio formulas. We only did one example in class because we didn't have much time left. That is everything.

Kenzie is next.

Fun With Vectors and Scale Diagrams

We started class today by reviewing  collinear vector addition, then proceeded to learn the "Tail to Tip" Method of vector addition. We used this method to add non-collinear vectors, which we are unable to add algabraically. The steps to create one of these wonderful diagrams include:

1. Write your scale and reference coordinates
2. Start by marking an "X"
3. Place your first vector's tail at the "X" (Remember to label it with the magnitude AND direction!)
4. Draw the next vector, starting at the tip (the arrow head) of the last vector. Continue to repeat this process with the rest of your vectors.
5. Draw a dotted line from the "X" to the tip of your final vector. This dotted line represents the Resultant Vector.
6. Use a ruler to measure the resultant vector. Determine its direction from the starting point ("X") using a protractor.

After taking notes, we practiced adding non-collinear vectors until the class ended.

Ex:






This link leads to an app which allows you to try addition of vectors
http://canu.ucalgary.ca/map/content/vectors/addition/simulate/twomethods/

or http://canu.ucalgary.ca/map/content/vectors/addition/simulate/simple/applet.html

Next up is Charlene

Vectors: In the Awesome World of Physics

Today during class we learnt that a vector is composed of a line segment drawn to scale with an arrowhead at the end of it.

• Collinear Vectors- both in same dimension. Ex. 3cm [N] + 6cm [S] = 3cm [S]
• Equivalent Vectors- exactly the same. Ex. 2cm [E] + 2cm[E] = 4Cm [E]
• Non- Collinear Vectors- more than one dimension. Ex. 11m [S] + 5m [W] = ???

Vectors can be added directly if collinear. A negative vector quantity indicates that its direction is actually opposite to that stated and that the sum of two or more vectors is called a Resultant Vector. 

Congratulations! Tessi can go next.

Determining 'g' on an incline lab

For todays class, we again went over the lab for the first maybe 10 minutes of class.  We then proceeded to finish it.  In this lab we place up to 5 books under the ramp and record it with the motion detector and LabQuest thing.  Yesterday we got up to 1 or 2 books and today was the rest, we calculated sine, and acceleration.  With the information we get from those we make a graph to get what the incline would be at sin90, or 1, which should equal to 9.8.  We used a new percent difference formula being the absolute value of accepted-experimental all over accepted multiplied by 100.  I guess that sums it up.

Next is Painter : )

Determining Acceleration Due to Gravity

We started off Tuesday's class by reviewing the Cart on a Ramp lab and going over any problems that we had. Some key concepts that were needed to complete the lab are:

• Know how to draw and describe position, velocity, and acceleration graphs.
• Have a good understanding of how to use the LabQuest, and to be able to curve fit the different types of graphs.
• Calculate the percent difference.

From this lab we learnt that an object on an incline that does not change will always have a constant acceleration due to the force of gravity.

After reviewing the Cart on a Ramp lab, we then started on a new lab, Determining g on an Incline. This lab consists of Mr. Banow saying extrapolate a few times, and changing the incline of the slope to help us determine the value of gravity (g). To do this we use the LabQuest, a ramp, the motion detector, and the dynamics cart.

Krystle goes next.

Finishing the Lab

Today, we started off by reviewing how to do the lab, more specifically, how to curve fit in the LabQuests, and rewriting the percent error formula.

We finished the lab from the previous two days, Cart on a Ramp!, by finishing any last information on Section I and moving on to section II.

Section II consisted of:

• re-rolling the cart so it bounced 3 or more times
• recording information and drawing the graphs for the roll
• Interpreting information such as slope and curve fitting to find if rolling sections were consistent.

My group found that it was indeed consistent, most likely due to gravity being a constant.

Next is Zach

Lab Continuation

In Friday's class we continued to work on our labs from Thursday where we used the motion detectors to find acceleration-time graphs, velocity-time graphs, and position-time graphs.  We used the graphs and interpret the results to answer the questions.

Brady is next.

Cart on a Ramp!

We did not go over the previous lesson because yesterday was pretty much a weekend and today was something new to work on. Today, we spent about half of the hour going over the blog posting and I was designated to be the first poster. After that we received a lab to work on involving a cart and a ramp.

• We looked at the distance, velocity, and acceleration of the cart moving up the ramp given a small push. 
• The preliminary questions were answered and gave our predictions on what we thought the graphs would turn out like, most groups also had their graphs printed off. 
• Procedure Part I was finished. 
• With this experiment we will figure out the position-time, velocity-time, and acceleration-time graphs which fits with our unit of kinematics. 
• We will also be able to see if the cart maintains a constant acceleration. 

Tomorrow looks to be more promising in content as today was mostly collecting data to analyze.

How to Post

This is so much fun! I love blogging.