Hooke's Law

Today in physics we reviewed what we did on Friday which was total energy and how the amount of kinetic energy and the amount of potential energy are always equal to the starting total energy.

We then moved on to look a springs, more specifically, Hooke's Law which contains stuff about the spring constant and how far from equilibrium the sping is depressed or stretched.

Ex: A compressed spring that obeys Hooke's law has a potential energy of 18 J. If the spring constant is 400 N/m, find the distance by which the spring is compressed.

Ep = 18 J

k = 400N/m

x = ?

Ep=1/2kx^2

=to find x we manipulate the formula to get the root of 2ep/k

= the root of 36/400

=3/10 or .30m the spring compressed.

We also looked at finding the total energy and the maximum height of an object, in this case, a golf ball.

Ex: Determind the total mechanical enerygy of a 48g golf ball if it has a velocity of 25 m/s when it leaves the club face.

m = .048 kg

vi = 25 m/s

hi = 0 m

et = 1/2mv^2

=1/2(.048)(25^2)

=15J

b) If the golf ball goes in an arc and has a speed of 15 m/s at its maximum height, what will the maximum height be?

h = ?

Et = 15 J

m = .048 kg

v = 15m/s

Et=mgh+1/2mv^2

15J=(.048kg)(9.8m/s^2)(h)+1/2(.048)(15^2)

And to find h we manipulate the formula and eventually get that the height is 20m.

Landon is next.

Roller Coasters!

You will be completing an assignment that uses the Physics of Energy to explain how a roller coaster works.

For Monday I need you to look over the following list of possible websites to use or to select a video that shows a roller coaster in action.  Choose a video or a program to use.
https://docs.google.com/document/d/1Q6nmNhSqJ6Nn-JXg7HFrjm7m_Gdja076XPdRKqFSu3U/edit

If you are using an online game/animation for your roller coaster, on Monday you will be given time on the laptop in the Physics Lab to make a video of your roller coaster in action.

On Tuesday we will go to the computer lab for you to view your video and come up with the explanation that you will present to the class.

On Wednesday, we will present them!

The general idea behind the assignment is:

Create a roller coaster. Use Smart Recorder to record it or save it if you can.

Present your video to the class. Pause the video as you go to explain the physics behind the motion:

Draw on the screen with the SMARTBoard

• key ideas:
• height
• velocity
• kinetic energy
• gravitational potential energy
• gravity
• use given or arbitrary values for the height to explain why the roller coaster works

Potential Energy and the Law of Conservation of Energy

Today in a heated and somewhat violent Physics class, we learned about potential energy and the law of conservation of energy. We started off by finishing the questions on kinetic energy we did the day before on page 290 #1-4

Then we read pages 291 and 292 in the textbook and answered questions about it.

From the reading we learned some new definitions:

Potential Energy- Energy that is stored and capable of being transformed into other types of energy.

Law of Conservation of Energy- Energy is not created or destroyed in any interaction, but is merely transformed from one type of energy into another.

Mr.Banow used the textbook as per usual to show us that when he holds the book above the floor and the book is not moving it has potential energy.

After the reading we moved on to learn about the most common type of potential energy and the one we will use most often in Physics 30 and that is Gravitational Potential Energy.

Gravitational Potential Energy- the energy stored as a result of the vertical position (height) of an object.

The formula to calculate Gravitational Potential Energy is Eg=mgh where:

Eg is Gravitational potential energy (J)

m is mass

g is acceleration due to gravity

h is change in height relative to the reference point

Ex.1

A 25.0kg box is lifted from the floor to a ridiculously large desk that is a whopping 1.87m above the floor.

a) What is the gravitational potential energy relative to the floor?

m=25kg

h=1.87m

g=9.8m/s^2

Eg=?

Eg=mgh

=(25kg)(9.8m/s^2)(1.87m)

=458J

Jeren (soon to be four eyes) Tuchscherererererererererererer is next

Review of Collisions

We reviewed yesterday's lesson again. It was on collisions. So, either elastic collision or inelastic collision.

Elastic collision- there is no change in kinetic energy after the collision has occured.

Inelastic collision- where some energy is 'lost' when colliding objects are in contact.

Mr. Banow showed us a whicked example of inelastic collision using two steel balls and a piece of paper.

First, he put one of the balls in the middle of a roll of tape and put the piece of paper on top of the ball. Next, he took the second ball and dropped it so it would hit the ball below the piece of paper.

What happened you may ask?

Well, a little hole was burnt into the piece of paper as well as a 'clunk' sound when the balls hit was made.

The reason why the collision of the two steel balls was inelastic because their was energy lost in the form of heat and/or sound. Not all of the energy was being conserved as kinetic energy.

We then did questions 1-4 on page 290.

Ryan Fly is up next.

Kinetic Energy

For some reason by pictures are up there ^^^^ but their relevance will be explained later. We started off class by reviewing the questions we started yesterday on power. These questions also reviewed calculating work quite nicely as we discovered that work needs to be calculated in order to solve for power.

Next, we expanded on what we had previously learned about energy. We we introduced to some new concepts:

1. Kinetic energy- the energy of motion. Ex: a ball rolling. Formula: $Ek=1/2mv^2$ Kinetic energy is a scalar quantity :)
2. Potential energy- the energy of rest. Ex: a ball being held in the air.
3. Change in energy= (final kinetic energy- initial kinetic energy) or $1/2(mvf^2-mvi^2)$

We learned that work= change in energy. This concept is important because it can make problem solving a lot easier. For example, we were given a problem that gave us the variables mass, initial velocity, and final velocity and were asked to solve for work. Instead of calculating force, displacement, and acceleration to eventually find work, we were able to simply calculate change in energy using $1/2(mvf^2-mvi^2).

Finally, we reviewed and expanded on our knowledge of collisions. We learned how energy fit into each type and were introduced to one new type:

• elastic collision- the two bodies don't stick together after the collision. There is no change in kinetic energy. Ex: the bat hitting the ball
• inelastic collision- the two bodies stick together after collision, some energy is lost. The energy lost is usually in the form of sound, heat, or light. Ex: the cars stuck together
• completely inelastic collision- the two bodies stick together after the collision but no energy is lost. Ex: the spaceship stuck in the planet.

Paige is next, I think.

Energy and Power

Monday we reviewed a bit of what we did on wednesday, we covered calculating work from a graph and when work is done by pulling something on a angle. We went over how work is produced: the force must be in the same direction as displacement to have work done.

What we learned on Monday was that when work is done, energy is transferred from one object to another. If the energy of an object increases, the work done on it will be positive. If the energy of an objects decreases, (ex. slowly bringing an object to the floor.) the work done on it will be negative.

Time has no effect when calculating work, but it does matter when we calculate power.

Power is the rate at which work is done and the rate at which energy is used. We calculate power in watts (W).... 1 watt is 1 J/s. Since watts are really small, we use kilowatts too (kW). To describe engines, the term horsepower is used. 1 horsepower equals 746 watts.

Things to Remember:

• P=W/t
• work is the product of force and the objects displacement (same direction)
• the less amount of time doing work, the more power being used (same displacement)
• to calculate kilowatt hours, multiply number of kilowatts by the number of hours used
• work is measured in joules (J)

Ex. 2. (in notes)

How much power is developed in lifting 82 kg of concrete to a height of 21 meters in 12 seconds?

m= 82kg
h= 21m (distance)
t= 12s
P=?
W=?
F=?

F= mg
F= 82kg x 9.80 m/s²
F= 803.6 N

W= Fd
W= 803.6N x 21m
W= 16 875.6J

P= W/t
P= 16 875.6J/12s
P= 1400W

Conservation of Momentum

The class began with the perpetual note-taking on the subject of Momentum; included in the aforementioned topic was the extended subtopic of the Conservation of Momentum. Various types of collision and explosion are included in the conservation of momentum—they are:

Explosion from Rest- One object splitting into multiple; given by the formula M1V1=-M2V2( and various manipulations of it).

Explosion from Motion-An object in motion, therefore with a initial velocity NOT of zero, splits into multiple objects; given by the formula (M1+M2)Vi=M1Vf1+M2Vf2

Elastic Collision-Two separate objects (with two separate masses and velocities) collide and rebound; given by the formula M1V1i+M2V2i=M1V1f+M2V2f

Inelastic Collision- Two objects colliding and becoming one; given by the formula M1V1i+M2V2i=(M1+M2)Vf

NOTE: All of these formulas can be derived remembering the Law of Conservation of Momentum, that is, initial momentum of an isolated system is equal to its final momentum, or the total momentum of an isolated system does not change.

Ex.)

A 95kg Unger collides while running 5.0m/s into a static Boss with a mass of 76kg. If Unger rebounds with a velocity of 3.0m/s, what is the velocity of the object he collided with?

M1V1i+M2V2i=M1V1f+M2V2f

M1=95kg

M2=76kg

V1i=5.0m/s

V2i=0.0m/s

V1f=3.0m/s

V2f=?

((95kg)(5m/s)-(95kg)(3.0m/s))/76kg=V2f=2.5m/s

We then continued with textbook questions on page 149, #1-5.

Whoever is left is next.

Momentum/Impulse

We started off class by finishing our notes from monday on Impulse. After we finished our notes we took up questions in our text books Page 243 #1-3.

Ex. What average force will stop a 1.0x10 3 car in 1.5s, if the car is moving at 22m/s?

m=1.0x10 3kg
deltaT=1.5s
vi=22m/s
vf=0
F=?

FdeltaT=mvf-mvi

F=-mvi/deltaT

F=-(1.0x10 3kg)(22m/s)/1.5s

=15,000N

When there was 10 minutes left in class Boss decided to take up more notes on
Law of conversation of Momentum
the total momentum of a closed system does not change.

An isolated system is one in which no net external force acts on the system
Momentum is conserved regardless of whether the iteractions exists in more than one dimension.

Then the bell rang and we ended off class with imcomplete notes that we will proabably take up today.

Mr. Banow has the power to pick who is next because i dont know who is left

Momentum

Momentum can be described as "inertia in motion." It is a vector quantity and the unit of momentum is kg * m/s.

Since the cannonball has more momentum than the cannon itself the cannon gets pushed backwards as the ball goes forward.

Ex.
What is the momentum of a 1.0x10^3kg car moving at 15m/s[E]?
m=1.0x10^3kg
v=15m/s[E]
p=?
p=mv
p=(1.0x10^3kg)(15m/s[E])
p=15000kg*m/s[E]

Impulse is simply the change in momentum. When an object experiences a force that causes it to speed up or slow down there is impulse.

When a golf club is about to hit a ball, the ball initially has zero momentum. After contact, the ball has momentum in the same direction as the force, and it also depends on how long the force acted upon the ball.

Ex.

What velocity will a 40.0kg child sitting on a 40.0kg wagon aquire if pushed from rest by a force of 75N for 2.0s?

m=40.0kg+40.0kg=80.0kg

F=75N

(delta)t=2.0s

Vi=0

Vf=?

F(delta)t=mvf-mvi

Vf=F(delta)t/m

Vf=(75N)(2.0s)/80.0kg

Vf=1.9m/s

Forces of Friction

We began by reviewing the subject matter from Friday, which concerned frictional forces...

• Static friction is defined as the friction that prevents a stationary object from beginning to move.
• Limiting static friction/Starting friction is defined as the maximum value of the force of friction that occurs just before the object starts to move.
• Therefore, if a force that is smaller than the limiting static friction is applied to a stationary object, the object won't move unless the force is increased and overcomes the limiting static friction, and once the object is in motion less force is needed to keep it in motion.
• is the formula used to determine the force of friction. As the mass increases, the Net Force increases, as well as the amount of friction.
• Without an applied force, a static frictional force does not exist.

We then did four examples that required us to utilize and manipulate the formulas concerning friction. Example one is shown below.

Ex.1) If the total weight of a skier and the skis is 500.0 N and a force of 35 N is needed to start the skier moving on the snow, determine the coefficient of static friction.

• We manipulate the formula to achieve 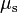= Ff/Fn
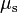• = 35 N/500.0 N
• Therefore, 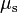= 0.070

Finally, we worked on practice questions from the textbook (Page 169, 1-4).

This link leads us to a video that explains the forces of friction in greater detail: http://www.youtube.com/watch?NR=1&v=cKUzHgBI_GY

Gbergz 360 is up next.

Friday November 4 - Frictional Forces

We started off class with a friday quiz on Newton's laws of motion, and then did some examples on the board.

After that we started talking about frictional forces. There are three kinds of frictional forces.

1) Static Friction - the friction that tends to prevent a stationary object from starting to move.

2)Limiting Friction - the maximum value of the force of friction which occurs just before the object starts to move. (starting friction)

3)Kinetic Friction: the force of friction that opposes the motion of a moving object. It is always less than the limiting static friction. (means that once the object starts moving the force of friction drops)

We then talked about the formula for the force of fricion $Ff=uFn$

u= Coefficient of friction (no unit)

Fn= Normal force (N)

Ff= Force of fricion

We finished the day talking about a problem with bricks and how the frictional force of a brick on its end is the same as a brick on its side.

Jolene is next.

November 4th Quiz Massacre!

The quiz results were not so great.  I am willing to Omit the quiz mark for you if you:

a. Fix up all of your quiz answers

b. Complete p. 156 #13, 17, 18.  These questions need to be answer clearly showing all of your steps and work.  I can't accept scribbles and the answer.

This must be submitted to me by Wednesday, November 9.  This will be a great way for you to re-practice this objective.

Gravitational Force

First we received our Newton's 2nd Law Investigation Labs, which we discussed why the %error was so high. We discovered that because we completely ignored the role of friction in the lab, it caused the over all result of the lab to be inaccurate. Mr. Banow than explained that we are to comment on his blog post and come up with a new and improved lab that will account for the friction.

We than began looking at Gravitational Force and learned three new definitions.

• Force of Gravity- objects are pulled toward the Earth no matter their location on or above the Earth's surface.



• Gravitational Field Constant- value is 9.8N/Kg and is represented by the letter g. This value is very close to being accurate anywhere on or near the Earth's surface.



• Gravitational Field Strength- the force of gravity is not the same everywhere therefore it is defined by the amount of force acting on a mass of 1Kg. For example there are different values on different planets.

Formula: F=mg

Example: The force of gravity on a 300.0Kg spacecraft on the moon is 489N. What is the gravitational field strength on the moon?

m=300.0Kg F=489N g=?

F=mg ----> g=F/m ----> g=489N/300.0Kg = 1.63N/Kg or 1.63m/s^2

Lastly we reviewed that mass and weight ARE DIFFERENT. Mass refers to the amount of matter in an object and stays the same no matter where it is. Weight describes the force of gravity on an object and changes depending on the gravitational field.

Jolene is next.

Newton's 2nd Law Lab - Going further!

In class we completed an investigation of Newton's Second Law.  Most of the data supported the fact that as the mass of the cart increased, the acceleration of the cart decreased.  Most of our data indicated that there was a lot of error in the calculated Net Force on the cart and the Theoretical Net Force acting from the mass hanging off the pulley.

Why was there so much error?

Could we do a new experiment to account for this error?

What would that experiment look like?  What could we add to the procedure?

Paige hasn't done this lab yet.  I need all of you in this class to be involved in a discussion about this topic.  Everyone must comment at least once on the questions above by this Friday.  Next week we will comment more and develop an experiment for her to do.  

• To start off the class we looked at Jeren's blog about Newton's third law of motion.


• We finished c) on example one of the notes finding out that we would add 22N to 121N to get 143N so it will overcome the force that is used by toboggan 2.


• We than got assigned practice questions on page 149, numbers 1, 2, 3a. Once done that we could finish assignment 6 that we got a few days ago. Once done those two assignments we could work on the review on page 155, numbers 8, 9, 11, 13, 17-20.

Page 149 Question #1

Two girls, one of mass 40 kg and the other of mass 60kg, are standing side by side in the middle of a frozen pond. One pushes the other with a force of 360N for 0.10s. The ice is essentially frictionless.

(a) What is each girl's acceleration?

Mg1-40kg Mg2-60kg Fa-360N T-0.10s

F=ma F/m=a 360N/40kg=a =9m/s^2 360N/60kg=-6m/s^2

(b) What velocity will each girl acquire in the 0.20s that the force is acting?

Vf=Vi+at =0+ 9m/s^2(0.10s)^2 = 0.9m/s

Vf=0+(-6m/s^2)(0.10s) = -0.60m/s

(c) How far will each girl move during the same time period?

d=Vi(t)+1/2(a)(t)^2 +1/2(9m/s^2)(0.10)^2 = 4.5 x10 ^-2 m

D=1/2(-6m/s^2)(0.10)^2 = -3.0 x 10 ^-2 m

2) Two crates of masss 12.0kg and 20.0kg, respectively, are pushed across a smooth floor together, the 20kg crate in front of the 12kg crate. Their acceleration is 1.75m/s^2. Calculate each of the following.

(a) the force applied to push the crates.

M1=12.0kg M2=20.0kg a=1.75m/s^2

F=(32.0kg)(1.75m/s^2) = 56.0N

(b) the action-reaction forces between the two crates.

F=(20.0kg)(1.75m/s^2) = 35.0N

Dana is next

Newton's Third and Best Law of Motion

• First of all, we got our quizzes back that we wrote unexpectedly on Friday then we learned about Newton's third law of motion which states: For every action force there exists a reaction force that is equal in magnitude but opposite in direction.
• After that we really didn't do much except a few examples on the third law of motion using F=ma and stating what the action or reaction was from an object doing something.

Ex: Badminton racquet hitting a birdie.

• Action: racquet force to birdie.
• Reaction: birdie applying force to the racquet.

Ex: Three toboggans are connected by a weightless, steel rope. The first toboggan has a mass of 75kg, the 2nd has a mass of 55kg, and the 3rd has a mass of 10.0kg. If the force exerted on the first toboggan is 310N and surfaces are considered to be frictionless, Find:

a) The acceleration of the toboggans.

F=ma changing the formula to a=f/m to find the acceleration. So it will be: a=310N/140Kg

=2.2m/s^2[E]

b) the force exerted by the toboggan two on toboggan three.

Again, F=ma in which F = ?, m = 10KG, and a = 2.2m/s^2 [E]

Therefore: F=(10KG)(2.2m/s^2[E])

=22N

c) the force exerted by toboggan one on toboggan two.

We will find out the true answer for this today in class, hopefully.

Blake is next.

Newton's 2nd Law with Vectors

Today we learned more about Newton's 2nd law dealing with vectors but first we had a discussion about smoking. Garrison said that all the cool kids smoke but Mr. Banow disagreed. Mr. Banow said that smoking is a bad habit and that drinking a glass of water would be much better.

Anyway we learned how to find the applied force on an object when the motion of the applied force was up and forward as so:




In order to find the applied force we first needed to find the x component of the vector by making sure we take the friction into consideration. Once we found the x component using the $Fnet=ma$ formula, where Fnet is the net force, m is the mass and a is the acceleration, we then used the angle given in the equation and the x component of the vector to find the value of the applied force vector.

This connected back to what we were doing in the vectors unit. We had to find the components of the vector to find the resultant vector, just like we did today.

Jeren Tuchschererererererererer is next.

Phun in Physics: Newton's 2nd Law Investigations

Once upon a time there was a group of high school students. Now this was no ordinary group of students.. they were a brilliant bunch and on this specific day found themselves having phun in physics with Mr. Banow!

The day started out with Daegan explaining the physics behind shooting a basketball. Rebecca followed by explaing the different serves in volleyball and the factors involved. We reviewed Newton's second law which states: if an unbalanced force acts upon an object then the object accelerates in the direction of force. The formula to accompany that is $Fnet=ma$

The class was given a lab to work on called Newton's Second Law Investigations. The goal of the lab is to determine whether an increase in the mass of an object affects the acceration of an object if the applied form is kept constant.

The class was divided into groups and the lab was set up like so:

To gain the correct data, each group had to measure how heavy their cart was without weights on it. The first trial went without any weight on top of the cart. Two time trials were made to gain accuracy and from that an average time was calculated. From the average time the acceleration was deducted and the Newtons (N). After initially having no weight on the cart, the groups had to add weight to the cart and calculate the results. This step was repeated 3 more times for a total of 5 trials. This was the end of the procedure part of the lab. Tomorrow the class will analyze the data and answer the corresponding questions.

Joey also corrected Unger's hairstyle...That is the story of the Physics 30 class!

The tale is to be continued by Ryan F :)

Acceleration as a vector quantity / Newton's Laws and forces

On Monday we learned about acceleration as a vector quantity. Acceleration is defined as the rate of change of velocity. We learned that you can find acceleration by using the formula a= change in velocity/change in time. We used this formula to do a question about a race car and then a text book question.

On Tuesday we started unit 3 which started off with Newton's Laws which explain the relationship between acceleration and force.

After talking about this we took notes on 4 forces.

1. Applied Force - force applied to an object.

2. Force of Gravity - the force that attracts things to itself.

3. Normal Force - force that is put on an object that is in contact with another object.

4. Friction Force - the force exerted by a surface an object moves on.

Once we discussed these we put them all together onto graphs called free body diagrams that show all the forces that acted on the object in the picture.

Berger is next.

Example's Day!

Today in class, we started the day off with one of the best presentations from Joey about chucking sauce. I think it is in the running's for a Nobel prize. (Below are great examples on the look of a saucer pass, and the out come of the saucer pass (Canadiens scoring))

After the great presentation we carried on with the example's from Wednesday. We answered some questions with swimmers swimming across some rivers.

ex. How long will it take her to swim across the river?

d=200m

v=1.80m/s

t=? t=d/v

t=200/1.80

=111 seconds.

We worked on questions similar to this for about 45 minutes. At the end of class we got our unit 2 review and were reminded that our test is Tuesday.

Paige is next.

Relative Motion and Frames of Reference

Today we started the class by listening to announcements, then looked at Brittney's and Garrison's wall posts. After that we read a writing in the textbook about Relative Motion and Frames of Reference.

Relative motion is the motion of an object, like a car, relative to another object, like the ground.

Example: The air speed of a small plane is 200. km/h. The wind speed is 50. km/h from the east (therefore, blowing west). Determine the velocity of the plane relative to the ground if the pilot keeps the plane pointing in the following direction :

East- pVa= 200.km/h [E] pVg= pVa + aVg
aVg= 50. km/h [W] = 200. km/h[E] + 50. km/h[W]
pVg= ? = 150. km/h [E]



Darren Drayke Unger is next.

Resultant Vectors

Today Mr. Banow started off the class by going over what happened on Friday. On Friday we had a sub and we wrote our quiz and did an example of vector resolution that was in our notes. Today we worked on the textbook questions that we were suppose to do on Friday. 
We did questions: 1, 2a)b), and 3a) on page 94
                            1-3 and 5 on pages 103 and 104

We were asked to have all of the textbook questions finished for Wednesday.

 
This is what our sketche can look like when we use the vector component method.

Vector Resolution

Today we started off with Lindsey's presentation on the physics of a football's flight. Next we corrected a quiz from Science 10 for Mr. Banow. We read the new blog post which was done by UNGER. Then we started the lesson for the day which was continuing the idea of vector resolution...

If vectors are not perpendicular, we can still add them algebraically by first breaking the vectors down into their x and y components.

You need to use your trig functions: sin and cos

$cos = x component$ $sin = y component$

Steps for Problems Needing Vector Resolution

1. Write down the given information and determine the angle for each vector. Call the angle sigma and measure it counterclockwise from the positive x-axis (principle angle).

2. Break each vector down into its x and y components

• x component of the vector is given by Vx = Vcos(sigma)
• y component is given by Vy = Vsin(sigma)

3. Add the collinear vectors algebraically. You will now have one y vector (positive means North) and one x vector (positive means East).

4. Use the Pythagorean Theorem to determine the magnitude of the resultant vector.

5. Use a trigonometric ratio to determine the angle of the resultant vector.

We did an example about a football player who ran 5.0 m[N36E], 12 m[N51W], and 15 m [S73E]. We had to determine the resultant vector. *Because our vectors aren't perpendicular to each other, we must use vector resolution. We did the example and Mr. Banow said "Yes it is a lot of work but, it is relatively easy if you understand it."

Jordan C. or Brittney is doing the next blog after their hardcore RPS match.

Algebraic Vector Addition and Multiplying

Today in class we learned like in math if there is a right triangle with can use trig functions or pythagorean theorem. we received a new formula.

We also refreshed our minds with the SOH CAH TOA and trig functions to solve the question with the dotted line was given to us.

ex. A sail boat sails 230km [E] and then 340km [N]. Determine the boats displacement.

(we drew out wh

at the instructions gave us, then connecting both ends with a dotted line. We measured the dotted line and found it degree, looking similar to this.)

We also learned how to multiply the vectors the solving portions in the exact same. The are just 3 different things.

-Magnitude is K|A|

-Units are in the product of K and A

-Direction is the Direction of A.

Overall we did some notes, couple equations. Mr. Banow was being a jokester and having a good old time.

GBergz360 is next.

FUN DAY! vector practice-scale diagrams

Today we touched up our skills and did examples of drawing out Vectors. We started out with an example we did on Monday with the bear, the crocodile and the hyena. We did five challenging vector practice examples where A=4km[N] B=6km[E] and c=5km[W25S]

1. A+B


2. 2A+B


3. A+C-B


4. B+C


5. C+A

Vectors can be added in any order, and that you can use this method to add any type and any number of vectors

Fun Fact: Ice cream is chinese food. and Mr. Banow is next. If he takes the option than Unger is next

Vector Addition 101

Today in class we began talking about Vector Addition. Any vectors may be added algebraically if they are collinear. The vector sum of 2 or more vectors is called the resultant vector. For example, 5cm [W], 7cm [W] and 3cm [E] can all be added together.

A negative vector means that it`s direction is exactly opposite of the direction it is stated. For example, -3cm [N] = 3cm [S].


Example 1: Determine algebraically the result vector of the picture below.
5km [N 43° W] + 4km [N 43° W] = 9km [N 43° W]

Adding Vectors Graphically
We add vectors graphically when the vectors are non-collinear; since they cannot be added algebraically.

Steps to adding vectors graphically:
1. Decide on a scale and draw your reference coordinate to the right of your page.

2. Indicate the starting point of your first vector with an X

3. Draw one of the vectors placing its tail at the X.
**Remember to label all vectors with a magnitude and a direction!**

4. Draw your next vector starting at the tip (the arrow head) of the previous vector you drew. Do this step until all the vectors in the question have been drawn.

5. Draw a dotted line from the X to the terminal point of your final vector. This new vector represents the vector sum (resultant vector).

6. Measure the resultant vector and determine its direction from the starting point X using a protractor.

Example 2: Sally walks 3km [S], 5km [E], 2km [S] and 4km [W]. Determine the resultant vector.

Jordan Grywacheski is up next.

Vectors

We started the day off by correcting the Kinematics pracitce quiz.

Then we started our new unit on Vectors.

The difference between vectors and scalor quantities is

Vectors

• need a direction

Scalor Quantities

• consist of a magnitue (ex. 6kg or 42m/s)
• the units have to be the same

We then took notes as an intro to vectors. The key points of these notes included.

• A vector is composed of a line segment drawn to scale with an arrowhead at one end.
• The length of a vector symbolizes its magnitude, and the arrowhead its length.
• The direction of a vector always need to be put in squar brakets.

KEY TERMS

Collinear Vectors are vectors that exist in the same dimension.

Equivalent Vectors are a special type of collinear vectors that are equal in magnitude and direction.

Non-Collinear Vectors are vectors that exist in more that one dimension.

We finished off the day practicing drawing vectors.

Brianne is next.

Constant Acceleration Problems

• We started off the class by reviewing how to change a velocity-time graph into a distance-time graph or an acceleration-time graph. The steps are as follows:
  

Distance-Time Graph

1) Find the displacement (area) of different time intervals on the velocity-time graph.

2) Plot several points based on the displacement found in part one.

3) Use your knowledge about velocity to connect the points. Ex: You have two points, one at 2.0s and the other at 5.0s. Look at the velocity-time graph to see if the velocity was constant or changing between 2.0-5.0s. If it was constant, connect the points with a straight line. If the velocity was increasing, connect the points with a positively curved line, etc.

Acceleration-Time Graph

1) Find the slope of several different time intervals on the velocity-time graph. The slope indicates the acceleration of the object.

2)Use the calculated slope to draw your graph. Ex: If you find the slope to be 7.5cm/s from 2.0-5.0s, draw a straight line on the acceleration-time graph at 7.5 on the y-axis from 2.0-5.0 on the x-axis.

3) Whenever there is a straight horizontal line on the velocity-time graph, there is no acceleration.

4) Keep in mind that the acceleration-time graphs drawn at a Physics 30 level don't wouldn't usually make sense in a real life situation.

• Next we moved on to some constant acceleration problems.
  


• Some important points to remember when solving acceleration problems are:
  i) We cannot calculate the answer properly unless the question states that the acceleration is uniform.
  ii) An object that starts from rest has a $V1$ of 0.
  iii) Whenever gravity is acting on the object in question, the object has an acceleration due to gravity of $a=9.8m/s^2$
  iv) When selecting the formula to solve the problem, you should list all of the known variables and the variable that you are trying to solve for. You should be able to select the proper formula simply by looking at which variables are present.
  v) Formulae can be manipulated
  


• We finished off the class by starting a work booklet. The booklet is composed of questions that analyze all of the graphs we have learned about thus far.

Landon is next.

Physics 30 Exam and Dates

Here is the constant acceleration applet we used in class: Here it is!

Here are the answers to the Module 5 Assignment that we worked on Tuesday. HERE

We are writing a Practice Exam in class on Wednesday. This is to be used as an assessment of where you need to improve before Friday's exam. Here is the answer key: PRAC ANSWERS

There is a Kinematics Exam on Friday, Sept. 30. The exam will cover everything we have done so far. Here are the answers to the review: PAGE 1 PAGE 2

If you complete the entire review (you must show work for the multiple choice) and get it signed by a parent/guardian you will receive a bonus mark on your exam.

Good luck!

Acceleration: Constant, Instataneous and the Various Formulae

The class started with Mr.Banow saying a enthusiastic good morning and Jordan talking about the physics behind a toy bow and arrow (unfortunately I was not here for the presentation and so am unable to repeat what was discussed. I'm also assuming Mr. Banow said hi!). Following his presentation he continued to shoot the arrow at Unger.

The previous day the class had begun to work on questions to do with acceleration. The questions were found on page 62, 67 and 69. On page 62, you had to find acceleration using the formula $a=(vf-vi)/(t2-t1)$. On page 67 you not only had to find acceleration but also instantaneous acceleration. That was accomplished by using the formula $a'inst=change in v/ change in t$. On page 69 a velocity vs time graph was given. The question asked that the graph given be converted into another two graphs: a distance vs time graph and a acceleration vs time graph. To create the distance vs time graph, the area of different sections needed to be found to make the points on the graph. To create an acceleration vs time graph the acceleration needs to be calculated [using the formula for acceleration]. The parts with slope indicate acceleration while those that are straight on the velocity vs time graph indicate that this is no acceleration and therefore are found at the x axis on the acceleration graph.



As seen on this graph, there is no acceleration for the first two seconds. On a velocity time graph this would be a straight line. From 2 to 4 seconds this indicates that the acceleration has changed. On the velocity time graph, this part would have a slope. The last section of 4 to 6 seconds indicates that there is no acceleration again. The velocity time graph would be a straight line again.

The class continued after the questions were completed and Mr.Banow turned on the handy dandy smart board. We then looked at constant acceleration formulas. No notes were taken but the class watched an applet to do with a car. The applet showed the different graphs that occured with different motions the car performed such as maintaing a constant velocity, speed and acceleration.



Example 1) A car going constant speed showed the following graphs-*note ignore the numbers from these graphs as they are taken from different source. The shape they create is what is to be observed!

Distance








Velocity








Acceleration





Example 2) When we changed the initial velocity of the car, had an acceleration of (-1) and changed the distance, the following graphs resulted:






Distance







Velocity







Acceleration





The class went back to looking at the formulas that were seen before the applet. The formulas given (found on the handout from yesterday) can only be used if the acceleration is constant! We began to go over the question on a handout dealing with acceleration that had a variety of formulas given. The best choice had to be chosen based on the information given and what you had to solve for. The Graphs on page 69 were announced due for tuesday at the end of class.



Jillian is next :)

Acceleration & the Motion of Cars- 09/23/11

Today's class began with a weekly quiz, which focused on determining velocity and various forms of acceleration through the use of a Velocity-Time graph. From the graph we were asked to find instantaneous acceleration (acceleration of an object at a specific time), average acceleration (the rate of change of an object's velocity per unit of time), instantaneous velocity (velocity of an object at a specific time), and displacement (the change in position of an object) by finding the area of the desired time period. The formulas for the aforementioned vector quantities are as follows:

Instantaneous Acceleration/Average Acceleration- Δv/Δt

Displacement (from a Velocity-Time Graph)- if the area is a triangle: (1/2)bh, if the area is a rectangle: lw

We also had to recognize negative acceleration (which occurred above the x axis and was therefore still a continuation in direction, as compared to negative acceleration which crosses the x axis and would represent a change in the direction).

For the remainder of the class, we continued to work on the Motion of Cars Investigation. With the data collected, we were able to draw graphs and address the accompanying questions; knowledge on the different types of acceleration, velocity, and how to determine displacement were key. We were required to draw Position-Time graphs, which we could create simply by looking at the data collected, as well as a Velocity-Time graph. To create the latter graph, we determine the instantaneous velocity for each point in time using the formula v= Δd/Δt. An example of a Velocity-Time graph can be seen below:

Amanda is next.

Motion of Cars Investigation Part II

Mrs. Smith was our sub today and we went through the instructions for the rest of the class. We were to work on the Motion of Cars Investigation assignment that we had started the day before.

The previous day we had already collected all the data, so we were to analyze it and construct Position-Time graphs for the pull back car and battery operated car.

The information that we collected yesterday was the time inbetween every 6 dot intervals (which was always 0.10 seconds), the displacement between every set of dot intervals, and the displacement between each set of dot intervals in relation to the starting point (0).

By analyzing these graphs, we could see if the cars were moving in uniform motion (moving in a constant direction and speed), or non-uniform motion (changing in direction or speed).

For example:

In this Distance-Time graph, one can see that the object is moving in uniform motion, because it is moving with a constant velocity in a constant direction.

In this Velocity-Time graph, one can see that the object is moving in non-uniform motion because it is not moving at a constant velocity.

The above graphs show how important it is to know the difference between Distance-Time graphs and Velocity-Time graphs. Although they may look the same, they could give you completely different answers.

This assignment and the graphs that we had to complete relates to what we have been learning about recently. For the past few days, we have been learning to analyze and construct Distance-Time graphs and Velocity-Time graphs. In the assignment we also have to do a quick sketch of an Acceleration-Time graph for the pull back car, and recently we have been learning about acceleration.

~Rebecca is next

Motion of Cars Investigation - 9/21/2011

We started off class by introducing a investigation focused on the motion produced by a battery operated car in comparison to the motion produced by a pull-back car. More specifically, the lab requires us to determine if each car produces uniform motion (where the object moves at a constant speed and in an unchanging direction), or non-uniform motion (where the object has an inconsistent speed or a changing direction). We will do this by examing the marks made by the ticker timer as the cars as pull the paper through the timer.


With Daegan and Unger to assist him, Mr. Banow ran through the procedure involved with collecting data for the investigation. Next, in groups of three we began collecting the appropriate data.

Procedure:
First, we had to calculate the number of marks that indicate a time lapse of .10 seconds. Because we know the frequency that we receive is 60. Hz, we can perform the following calculation:

P=1/f
P=1/60. Hz = 0.016666666
0.016666666 x 6 dot intervals = 0.10


Therefore, in a time lapse of .10 seconds, the ticker tape produces 7 marks, and 6 dot intervals.

• Then, in groups of three, we cut a piece of recording timer tape to about 2 m long, and plugged in the recording timer and placed it on one end of the table.


• We inserted the timer tape into the timer, and used masking tape to secure the recording tape to the back of the pull-back car.


• One group member held the loose end of the recording tape, ensuring it passed through the timer correctly, while the second person was responsible for turning the recording timer on, and the third group member was responsible for winding up the pull-back car.


• Once the tape had passed through the timer, the tape was detatched from the car and the same process was done with the battery operated car.


• Each group then began to analyze the markings on each piece of tape, in order to determine what kind of motion each car had.

Lindsey is next.

Average, Instantaneous and Constant Acceleration

To start off class we went over the answers from the Assignment 4 hand-out.

We then went over a new topic... Acceleration!

Average Acceleration- the speed in which something is getting faster or slower.
We can find the average acceleration by using this formula:












or Vf-Vi

Vf or V2 being the final velocity of an object.
Vi or V1 being the initial velocity of an object.

*The SI unit of acceleration is m/s2 (squared) because an object increases speed by Xm/s every second.*

If an object is speeding up it would have a positive acceleration.
If an object is slowing down it would have a negative acceleration.
If an object is travelling at a constant velocity it would have zero acceleration.


Ex.
If you're riding in a vehicle and the vehicle starts speeding up (positive acceleration), you could notice this acceleration by looking at the speedometer but, also you could feel yourself being pulled back.
If the vehicle is slowing down (negative acceleration) you could feel yourself jerk forward.

You can find average acceleration on a graph by drawing a line from one point to another and finding the slope.

Instantaneous Acceleration- acceleration of an object at a specific time.

You can find instantaneous acceleration by drawing a tangent on a curve and finding the slope.

Constant Acceleration- object's velocity changes by equal amounts in equal periods of time.

We finished off class by doing four example questions on acceleration.



Jolene is up next.

Velocity and Time Graphs Part II

Todays class was basically a review of what we did on Friday. We started off by doing the questions out of the text book which asked us to find the displacement and velocity of different graphs.

• Displacement- find the area of the graph by using either 1/2bh (triangle) or lw (rectangle). Once you find the area add them together and that will give you the total dispacement. Remember if the graph has changed direction (gone below the x- axis) the area has to be subtracted.


• Velocity- finding the velocity of a specific point can simply be read off the graph. To find the velocity between two points you must first find the displacement or area of the graph, than by dividing that answer by the amount of time between the points it will give you the velocity.
  

Lastly after we were all finished the questions from the text book we were to complete the Assignment 4 Handout which was based upon the same types of questions.

Paigery Crozon is next :)

Velocity and Time Graphs

We started the day off with taking a quiz on displacement and distance and time graphs.

We learned how to do a velocity and time graph.

From the left of the graph 0-10 seconds shows that it is accelerating. From 10 to 15 seconds it is going a constant speed of 60m/min. From 15 to 30 seconds it is slowing down and at 30 seconds comes to a stop. From 30 - 40 seconds it changes directions and speeds up. From 40- 50 seconds it slows down.

We also learned that to find the displacement you divide the lines and the 0m/min line into triangles and rectangles using the formulas 1/2bh and lw. Once you get the numbers for the sections you addd them together. If the line goes below 0m/min tha you would subtract that section from the secton that is above the line.

We also learned how to switch a distance and time graph into a velocity and time graph and that they would look different but mean the same.

Dana is next.

We started class off with a presentation from Ms. Witte, who showed us the physics behind a tennis ball.

After the presentation we checked out Jeren's blog and discussed it.

After the blog we worked on finishing the questions out of the text book and if this was completed we worked on the sheets given in the previous class. Both the questions from the book and the questions on the sheets were about the slopes and velocities of graphs. To find such things we looked at the graphs and found out the rise over run and did the mathematical equation to find the velocities.

Mr. Rath is next.

Analyzing Position vs. Time Graphs

Yesterday’s lesson started out with Blake doing his presentation on the yo-yo and the physics behind it and how it works. We then moved on to a handout that we had gotten about position vs. time graphs. There were three graphs which were all different. They were connected to the previous classes because we have been looking at position vs. time graphs for awhile now and also some of the formulas we have been using such as displacement and velocity.

The first graph we were given the points and had to construct it ourselves. We then had to do the following things with the corresponding graph:

• Describe the motion of the graph by examining the lines on the grid; whether it was a constant positive velocity or not moving.
• We had to find the objects displacement which can be found by taking the ending positing and subtracting it by the initial position.
• We also then examined the graph to find which part of the trip was the fastest.

The second graph was another distance vs. time graph and with this one we had to:

• Find the velocity over each time interval and then find the average velocity over the entire graph. Velocity is equal to distance divided by the time and average velocity is equal to total distance divided by total time.

The last graph that we looked at was a distance vs. time graph which had a curve in it. We had to do the following:

• Find the instantaneous velocity at PT. A where you draw a tangent line so it barely touches the point on the graph. We then find 2 points such as (3,4) and (5,6). We will then find the slope of the graph which is equal to y2-y1 divided by x2-x1.
• The last part we had to find the average velocity of the graph where we had drawn a line straight across point b to point d, found 2 points on the line and found the slope of those points and that had given us the answer.

There was then some textbook questions at the end

Position vs. Time Graphs Sept. 13 2011

The main part of the lesson today was about position vs. time graphs but at first we did an example equation that dealt with the lesson from the day before. It was connected to speed and velocity but was a bit harder than the others we had done before. The question had three velocities and times in different directions and wanted the average velocity of the three. We needed to find the displacement of the three velcoities then divide by the total time to get the answer.
Next we looked at position and time graphs. Looking at these graphs connected back to what we had worked on last week. We had to graph the speed of and object and analyze the slope of the line. Today we looked at some of the basic rules with position and time graphs. We leanred that the slope of the line gives us the object's velocity which we had figured out last week. We learned that the slope of a line segement between two points on the line tells us the average velocity during that period of time. We also learned that the slope of the tangent touching a certain point on the line tells us the instantaneous velocity at that certain time. We also looked at a few different types of position vs. time graphs. There is the zero velocity graph which is a horizontal line across the graph telling us that the object is not moving. Another graph is the constant velocity graph which is a straight line that shows us the velocity does not change as the object moves. Another example of a position vs. time graph is the continuously changing velocity graph. This graph is a parabolic graph and the average speed of the object graphed by this line has changing velocity as it moves.

unger

Hi I'm Unger

Wow, you are taking Physics 30! Awesome!

You have found our class website. You may want to bookmark this page.

We will mainly use this blog to summarize each of our lessons. At the end of each unit it will serve as a great summary and review of what we have covered.

I encourage you to take this seriously as a useful tool to improve achievement. If you do, I think you will find that this is a great resource.